Nước là một chất có rất nhiều tính chất lạ, khác với nhiều chất khác. Nhiều tính chất của nước rất quan trọng cho sự sống (ví dụ như khối lượng riêng của nước đá nhỏ hơn nước ở trạng thái lỏng, làm cho các hồ ao chỉ đóng băng một lớp ở trên). Hôm nay trong Phòng đọc ta đọc về một tính chất của nước đá, có lẽ không quan trọng cho sự sống nhưng rất cơ bản, gọi là entropy dư thừa (residual entropy).
Trong nhiệt động học cổ điển, thường người ta không định nghĩa entropy mà chỉ định nghĩa độ thay đổi của entropy:

trong đó là lượng nhiệt ta truyền vào hệ. Nhưng từ thời Nernst và Planck người ta đã biết là có thể định nghĩa entropy một cách tuyệt đối: định luật 3 của nhiệt động học cho biết là entropy của tất cả các chất đều tiến đến 0 khi nhiệt độ tiến đến không. Dùng định luật này, nếu ta đo được nhiệt dung C của các chất như một hàm số của nhiệt độ, ta có thể tìm được entropy tuyệt đối:
là lượng nhiệt ta truyền vào hệ. Nhưng từ thời Nernst và Planck người ta đã biết là có thể định nghĩa entropy một cách tuyệt đối: định luật 3 của nhiệt động học cho biết là entropy của tất cả các chất đều tiến đến 0 khi nhiệt độ tiến đến không. Dùng định luật này, nếu ta đo được nhiệt dung C của các chất như một hàm số của nhiệt độ, ta có thể tìm được entropy tuyệt đối:

Nhưng nước đá dường như là một ngoại lệ. Nếu ta tìm entropy tuyệt đối của nước bằng cách đo đạc nhiệt tỏa ra trong các phản ứng hóa học, ví dụ , và từ entropy của H2 và O2 thì ra một con số, nhưng nếu tính ra từ công thức ở trên thì lại ra một con số nhỏ hơn! Sự chênh lệch khá nhỏ (188.65 J/K/mol so với 185.25 J/K/mol), nhưng vượt quá sai số của thực nghiệm. Dường như đối với nước đá định luật 3 của nhiệt động học không đúng và công thức trên phải thay bằng
, và từ entropy của H2 và O2 thì ra một con số, nhưng nếu tính ra từ công thức ở trên thì lại ra một con số nhỏ hơn! Sự chênh lệch khá nhỏ (188.65 J/K/mol so với 185.25 J/K/mol), nhưng vượt quá sai số của thực nghiệm. Dường như đối với nước đá định luật 3 của nhiệt động học không đúng và công thức trên phải thay bằng

trong đó là entropy của nước đá ở nhiệt độ không tuyêt đối và có giá trị là 3.4 J/K/mol. Đại lượng này được gọi là entropy dư thừa (residual entropy).
là entropy của nước đá ở nhiệt độ không tuyêt đối và có giá trị là 3.4 J/K/mol. Đại lượng này được gọi là entropy dư thừa (residual entropy).
Năm 1935 Linus Pauling đưa ra cách giải thích entropy này. Pauling là một nhà hóa học nổi tiếng có rất nhiều đóng góp cho hóa học (lý thuyết liên kết hóa học) và sinh vật học (tìm ra alpha helix trong cấu trúc protein). Ông ta được 2 giải Nobel, 1 về hóa học và 1 về hòa bình. Công trình của ông ta về entropy của nước đá ít nổi tiếng hơn nhưng cũng rất hay. Để minh họa, ta tưởng tượng nước đá là tinh thể 2 chiều, để vẽ cho dễ. Mô hình dưới đây ta sẽ tạm gọi là “nước đá vuông”.
Một tinh thể nước đá vuông phải có những tính chất sau:
1. Các nguyên tử oxy làm thành một mắt lưới vuông (xem hình dưới).
2. Trên mỗi đoạn thẳng nối giữa hai nguyên tử oxy lân cận có một và chỉ một nguyên tử hydro. Nguyên tử hydro không nằm ở chính giữa, mà gần 1 nguyên tử oxy hơn nguyên tử kia (trong tinh thể nước thật, khoảng cách từ một nguyên tử hydro đến 2 nguyên tử oxy ở hai đầu là 0.10 nn và 0.18 nn).
3. Xung quanh mỗi nguyên tử oxy có đúng 2 nguyên tử hydro ở gần, 2 hydro ở xa.
Tinh thể nước không phải là vuông như vậy; các nguyên tử oxy nằm ở tâm hình tứ diện đều có đỉnh là các nguyên tử oxy lân cận. Nhưng điều quan trọng là mỗi oxy có 4 oxy láng giềng, và hydro nằm trên các đường nối.
Hình ở dưới là một cấu hình ví dụ, thỏa mãn tất cả các điều kiện trên:

nhưng nếu các bạn thử vẽ ra thì sẽ thấy hằng hà sa số các cấu hình thỏa mãn cả ba điều kiện ở trên. Nói cách khác, theo Pauling ngay ở nhiệt độ rất thấp khi các chuyển động bị đông lạnh lại thì vẫn còn một sự hỗn độn trong cấu trúc của nước đá. Pauling đánh giá số lượng cấu hình thỏa mãn ba điều kiện trên là , trong đó
, trong đó 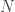 là số lượng phân tử nước. Nhưng entropy là log của số trạng thái vi mô, do đó ở entropy còn lại của nước đá khi nhiệt độ xuống rất nhỏ là
là số lượng phân tử nước. Nhưng entropy là log của số trạng thái vi mô, do đó ở entropy còn lại của nước đá khi nhiệt độ xuống rất nhỏ là
 J/mol/K
J/mol/K
hoàn toàn phù hợp với thực nghiệm. Đánh giá số cấu hình của Pauling sau này được chỉ ra là không hoàn toàn chính xác, nhưng rất gần với con số thật, (J. Nagle, J. Math. Phys 7, 1484 (1966)). Các bạn đọc những trang trong cuốn giáo trình hóa lý của Chang để biết Pauling đánh giá như thế nào.
(J. Nagle, J. Math. Phys 7, 1484 (1966)). Các bạn đọc những trang trong cuốn giáo trình hóa lý của Chang để biết Pauling đánh giá như thế nào.
Gần đây các nhà vật lý chất đậm đặc rất quan tâm đến một trạng thái gọi là spin ice, có entropy dư thừa về bản chất cũng giống nước đá, nhưng sự hỗn độn trong đó là sự hỗn độn về hướng các spin.
Còn số phận của định luật thứ 3 của nhiệt động học ra sao? Tôi tin là nó sẽ vẫn còn đúng, nhưng trong trường hợp nước đá thì ta phải hạ nhiện độ xuống rất thấp thì entropy mới bằng không. Tôi chắc là tương tác giữa các nguyên tử hydro, cộng với các hiện tượng lượng tử (như hiệu ứng đường hầm) sẽ làm cho trạng thái cơ bản của nước đá chỉ có một, và entropy bằng không. Nhưng tôi không biết là ở nhiệt độ nào.
Trong nhiệt động học cổ điển, thường người ta không định nghĩa entropy mà chỉ định nghĩa độ thay đổi của entropy:
trong đó
Nhưng nước đá dường như là một ngoại lệ. Nếu ta tìm entropy tuyệt đối của nước bằng cách đo đạc nhiệt tỏa ra trong các phản ứng hóa học, ví dụ
trong đó
Năm 1935 Linus Pauling đưa ra cách giải thích entropy này. Pauling là một nhà hóa học nổi tiếng có rất nhiều đóng góp cho hóa học (lý thuyết liên kết hóa học) và sinh vật học (tìm ra alpha helix trong cấu trúc protein). Ông ta được 2 giải Nobel, 1 về hóa học và 1 về hòa bình. Công trình của ông ta về entropy của nước đá ít nổi tiếng hơn nhưng cũng rất hay. Để minh họa, ta tưởng tượng nước đá là tinh thể 2 chiều, để vẽ cho dễ. Mô hình dưới đây ta sẽ tạm gọi là “nước đá vuông”.
Một tinh thể nước đá vuông phải có những tính chất sau:
1. Các nguyên tử oxy làm thành một mắt lưới vuông (xem hình dưới).
2. Trên mỗi đoạn thẳng nối giữa hai nguyên tử oxy lân cận có một và chỉ một nguyên tử hydro. Nguyên tử hydro không nằm ở chính giữa, mà gần 1 nguyên tử oxy hơn nguyên tử kia (trong tinh thể nước thật, khoảng cách từ một nguyên tử hydro đến 2 nguyên tử oxy ở hai đầu là 0.10 nn và 0.18 nn).
3. Xung quanh mỗi nguyên tử oxy có đúng 2 nguyên tử hydro ở gần, 2 hydro ở xa.
Tinh thể nước không phải là vuông như vậy; các nguyên tử oxy nằm ở tâm hình tứ diện đều có đỉnh là các nguyên tử oxy lân cận. Nhưng điều quan trọng là mỗi oxy có 4 oxy láng giềng, và hydro nằm trên các đường nối.
Hình ở dưới là một cấu hình ví dụ, thỏa mãn tất cả các điều kiện trên:

Một cấu hình ví dụ của tinh thể nước đá vuông. Các hình tròn đỏ tượng trưng cho các nguyên tử oxy, hình tròn xanh là nguyên tử hydro. Các đường đen liên tục nối các nguyên tử trong cùng một phân tử nước H2O. Các đường đứt đoạn tượng trưng cho các mối liên kết hydro.
nhưng nếu các bạn thử vẽ ra thì sẽ thấy hằng hà sa số các cấu hình thỏa mãn cả ba điều kiện ở trên. Nói cách khác, theo Pauling ngay ở nhiệt độ rất thấp khi các chuyển động bị đông lạnh lại thì vẫn còn một sự hỗn độn trong cấu trúc của nước đá. Pauling đánh giá số lượng cấu hình thỏa mãn ba điều kiện trên là
hoàn toàn phù hợp với thực nghiệm. Đánh giá số cấu hình của Pauling sau này được chỉ ra là không hoàn toàn chính xác, nhưng rất gần với con số thật,
Gần đây các nhà vật lý chất đậm đặc rất quan tâm đến một trạng thái gọi là spin ice, có entropy dư thừa về bản chất cũng giống nước đá, nhưng sự hỗn độn trong đó là sự hỗn độn về hướng các spin.
Còn số phận của định luật thứ 3 của nhiệt động học ra sao? Tôi tin là nó sẽ vẫn còn đúng, nhưng trong trường hợp nước đá thì ta phải hạ nhiện độ xuống rất thấp thì entropy mới bằng không. Tôi chắc là tương tác giữa các nguyên tử hydro, cộng với các hiện tượng lượng tử (như hiệu ứng đường hầm) sẽ làm cho trạng thái cơ bản của nước đá chỉ có một, và entropy bằng không. Nhưng tôi không biết là ở nhiệt độ nào.
Nguồn bài viết: Blog của giáo sư Đàm Thanh Sơn













0 Comments: